Using and Evaluating Logistic Regression in R

Introduction

​​Hello and welcome to this deep-dive on Logistic Regression—one of the fundamental algorithms in the data science toolkit. I will be going through a simple example of how to implement and evaluate Logistic Regression that you can apply to practical applications.

​What is Logistic Regression?

At its core, Logistic Regression is a statistical method for modeling the relationship between a binary ( one or zero) outcome and one or more independent variables. Unlike Linear Regression, which predicts a continuous outcome, Logistic Regression is the go-to technique for classification problems—think yes/no or true/false type questions.

Imagine you're a bank trying to predict whether a loan applicant will default or not. You'd have several variables like income, credit score, and employment history. Logistic Regression helps you take all these variables into account to predict a 'Yes' or 'No'—will the applicant default?


You can also think of a similar example where you might want to recommend a product to a customer - is this customer likely to buy the product if they were recommended it? 

​What are we doing here? 

In this guide, we're going to get hands-on with Logistic Regression. I'll walk you through some code, step-by-step, to show you how to implement this algorithm from scratch. We'll take a practical approach, starting with data preparation, moving onto the math behind the model, and finally implementing it using R. I will present another tutorial with Python where we can utilize SMOTE and other techniques to assist with class imbalances. 

You're going to import a popular dataset for this problem found here: https://archive.ics.uci.edu/dataset/144/statlog+german+credit+data

Getting Started: Laying the Groundwork

Before we dive into the modeling, it's crucial to set the stage with some Exploratory Data Analysis (EDA). While the scope of EDA can be extensive in real-world applications, we'll focus on the essentials here to ensure our data is model-ready. Although we know this dataset is already cleaned up for us, we will still do an overarching EDA step. 

  • Null Values: Data gaps can throw off our model, so we'll look for any missing information.
  • Duplicates: Redundant data can skew results, so we'll eliminate any duplicates.
  • Distributions: Understanding the shape of our data helps us know if any transformations are needed.
  • Collinearity: Highly correlated variables can muddy our results, so we'll examine potential collinear relationships.

​What We'll Cover:

Though this guide won't delve into every nuance of building a robust model, we will touch on foundational evaluation metrics such as:
  • ROC (Receiver Operating Characteristic) Curve: To visualize the trade-offs between sensitivity and specificity.
  • AUC (Area Under Curve): To summarize the model's performance in a single value.
  • Basic Confusion Matrix: To give us a snapshot of how well our model is doing in terms of false positives, false negatives, etc.

Lets load the data

We are going to apply data that determines whether or not someone should be denied for a loan based on their features. The target variable is renamed 'target' for easy referencing

​germancredit <- read.table("germancredit.txt", header=FALSE, sep=" ") 
data <- germancredit

​Rename Columns

You'll see later down the line that there isn't really a necessity to rename the columns and then make dummy variables manually out of them. R does that automatically - but this method at least shows the steps we took to achieve this. I renamed these columns to be useful in future iterations for things like looping and for readability purposes. 

​new_names <- c("existing_checking_C",
               "Duration_I",
               "Credit_hist_C",
               "Purpose_C",
               "Cred_Amt_I",
               "Savings_C",
               "Employed_Dur_C",
               "Rate_I",
               "Status_Sex_C",
               "Debt_C",
               "Residence_I",
               "Property_C",
               "Age_I",
               "Installment_Plans_C",
               "Housing_C",
               "Open_Credit_I",
               "Job_C",
               "Dependents_I",
               "Telephone_B",
               "International_Employee_B",
               "Target")
colnames(data) <- new_names

Remove Duplicates (If any)

​data <- unique(data)

Check for Nulls

Missing values can create a lot of problems when running machine learning algorithms. Let's check for any nulls in the dataset.

​null_count <- sapply(data, function(x) sum(is.na(x)))
print(paste("Null values by column: ", null_count))

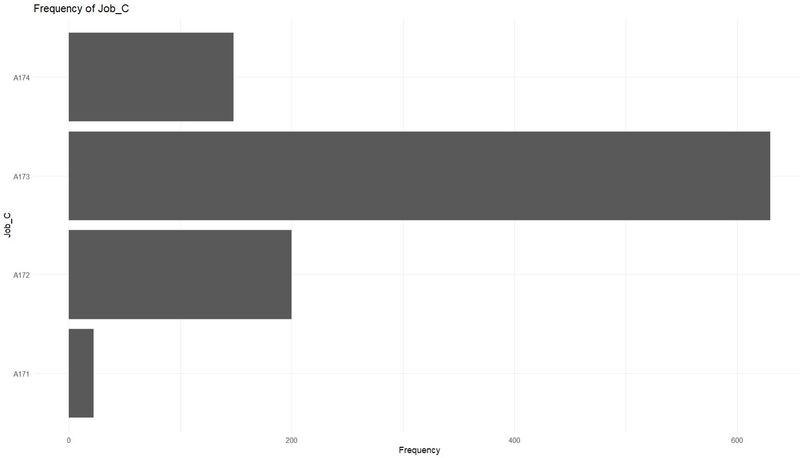
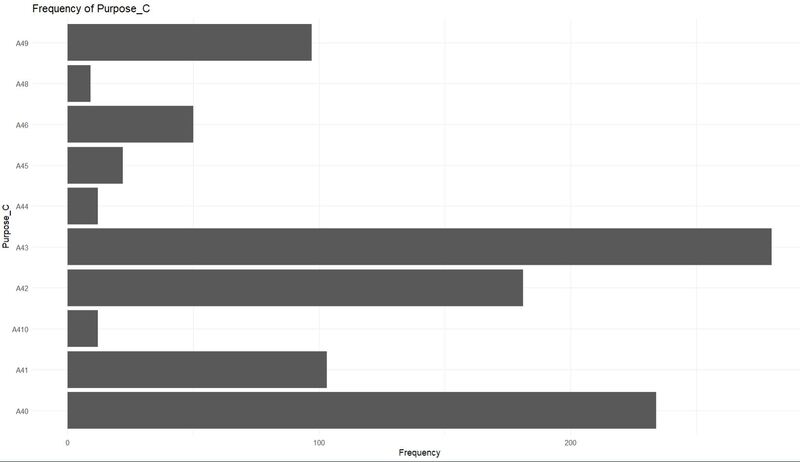
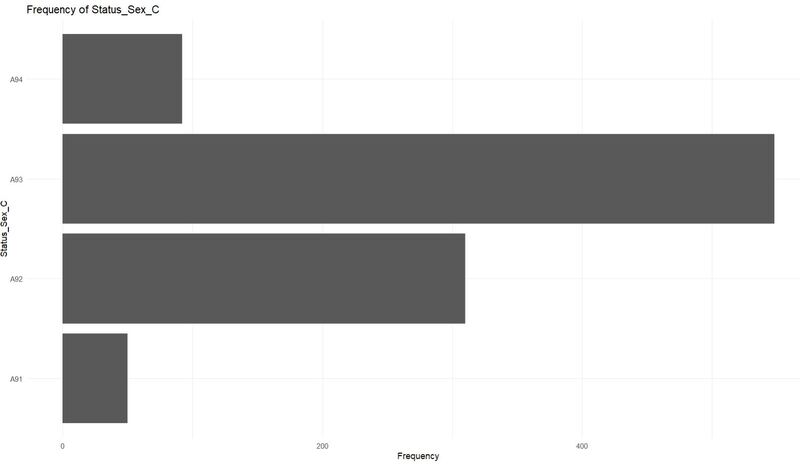
​Exploratory Data Analysis (EDA) - Categorical Variables

Before diving into building the model, let's do some basic EDA. First, we'll focus on the categorical variables. Overall, this is a very base-line way of doing some on-the-spot EDA. In a real business scenario, you need to understand the context of what you are trying to achieve and you also need to be aware of any potential drawbacks with using some of these categories to make predictions. 

​library(ggplot2)
cat_cols <- grep("_C$", colnames(data), value = TRUE)

for(col in cat_cols) {
  p <- ggplot(data, aes_string(col)) +
    geom_bar() +
    labs(title = paste("Frequency of", col), x = col, y = "Frequency") +
    theme_minimal() +
    coord_flip()
  print(p)
}

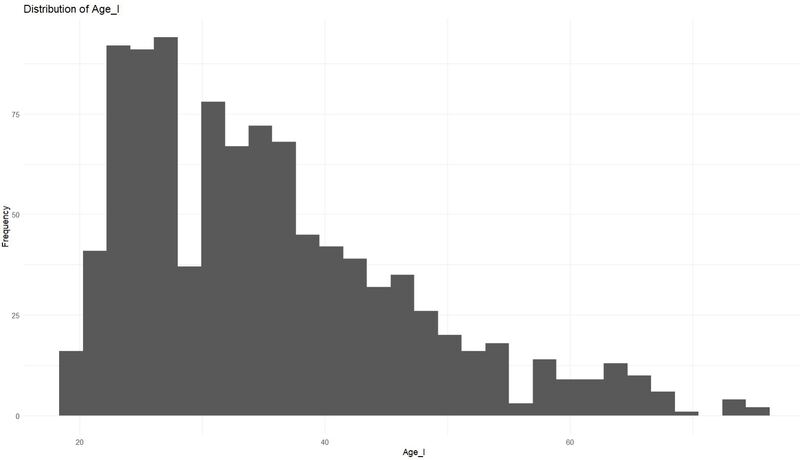
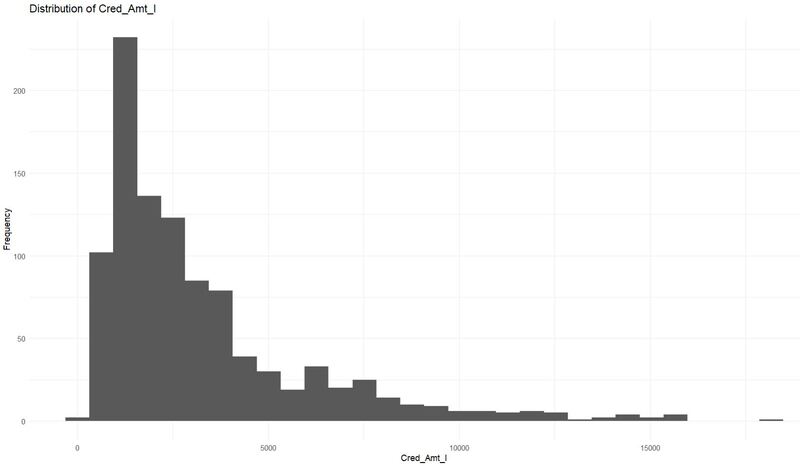
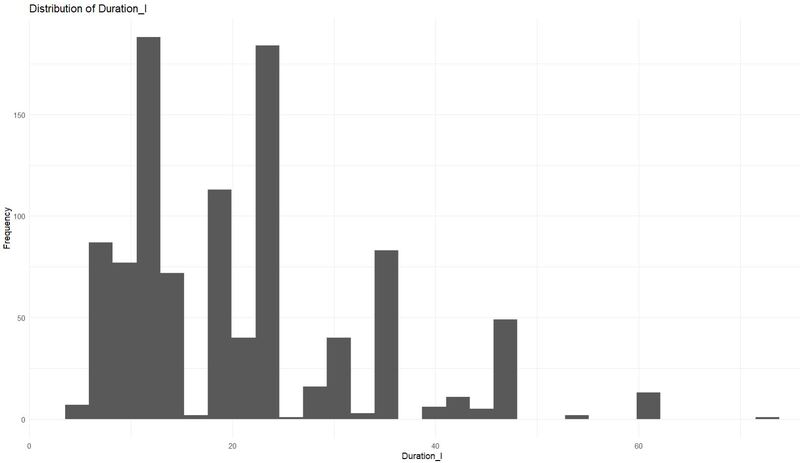
You should get an expected output like this detailing the distribution of values based on their category

Exploratory Data Analysis (EDA) - Integer Variables

​int_cols <- grep("_I$", colnames(data), value = TRUE)

for(col in int_cols) {
  p <- ggplot(data, aes_string(col)) +
    geom_histogram(bins=30) +
    labs(title = paste("Distribution of", col), x = col, y = "Frequency") +
    theme_minimal()
  print(p)
}

​Check for Collinearity

​library(caret)
correlation_matrix <- cor(data[, int_cols], use = "pairwise.complete.obs")
highly_correlated <- findCorrelation(correlation_matrix, cutoff = 0.75)
print(paste("Columns with high collinearity: ", colnames(data)[highly_correlated]))

The output here should be blank because the data was cleaned and prepared from the website.

​Encode Categorical Variables

Before we can build a machine learning model, we need to convert our categorical variables into a format that can be provided to machine learning algorithms to do a better job in prediction. For this, we use one-hot encoding. Here we're using the fastDummies package.

The reason we do not numerically encode the variables is because this may introduce an issue where a feature labeled as "2" would be considered as 2x more than the feature labeled "1"

library(fastDummies)

data_encoded <- dummy_cols(data, select_columns = cat_cols, remove_first_dummy = TRUE, remove_selected_columns = TRUE)

We want to remove the first dummy variable in our data. This is because it can lead to collinearity when we create dummy variables from each category in our sample. 

For instance, imagine we have 3 categories, Red, Green, and Blue.
If our data is set up so that each category has a binary column telling us if there is a red, green, or blue color it would lead to a problem. 

If we know that red and green are 0, we know for a fact that blue has to be 1. 
Same goes for any other relationship with the colors. So if we remove one of the columns - we would still maintain all the information while removing an extraneous variable.

​Update Binary Variables

Some of the variables in the dataset are binary but have been labeled with categories. For example, the Telephone_B and International_Employee_B columns have character values that we'll convert to numerical binary (0 or 1).
First, let's confirm the data type and unique values for these columns.

levels(data_encoded$Telephone_B)
levels(data_encoded$International_Employee_B)

class(data_encoded$Telephone_B)
class(data_encoded$International_Employee_B)

unique(data_encoded$Telephone_B)
unique(data_encoded$International_Employee_B)

Now we can update these columns! 

data_encoded$Telephone_B[data_encoded$Telephone_B == "A192"] <- 1
data_encoded$Telephone_B[data_encoded$Telephone_B == "A191"] <- 0
data_encoded$Telephone_B <- as.numeric(data_encoded$Telephone_B)

data_encoded$International_Employee_B[data_encoded$International_Employee_B == "A201"] <- 1
data_encoded$International_Employee_B[data_encoded$International_Employee_B == "A202"] <- 0
data_encoded$International_Employee_B <- as.numeric(data_encoded$International_Employee_B)

Update the Target Variable

The target is labeled as a 2 or a 1, and we need to update it to be a 1 or a 0 instead. 

data_encoded$Target <- data_encoded$Target - 1

We are now ready to begin modeling. The most important thing to do before applying any kind of model is pre-processing and cleaning the data. The next steps involve splitting the data into training and validation, and then evaluating the performance. 

Splitting the Data into Training and Validation

Before building any machine learning model, it's crucial to split your dataset into training and validation subsets. The training data is used to build the model, and the validation data helps us evaluate its performance. We'll use the caTools package to help with this.

install.packages("caTools")
library(caTools)

set.seed(123)  # Setting a seed for reproducibility
splitIndex <- sample.split(data_encoded$Target, SplitRatio = 0.7)

train_data <- data_encoded[splitIndex, ]
validation_data <- data_encoded[!splitIndex, ]

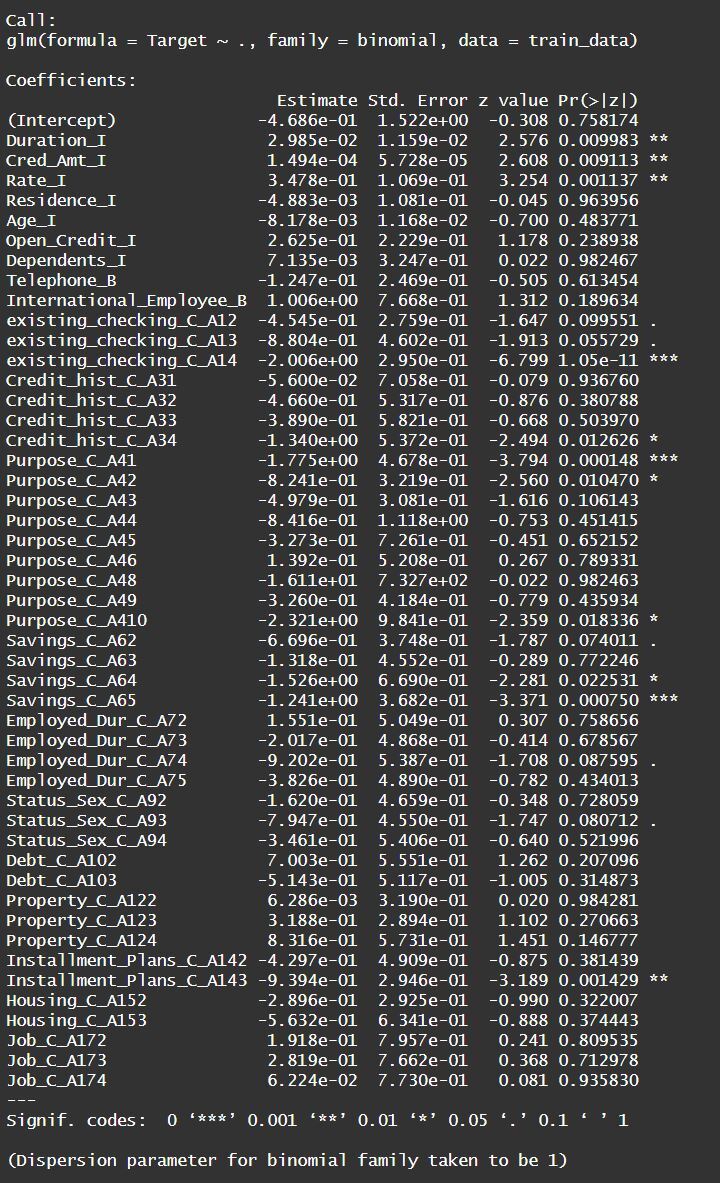
​Building the Logistic Regression Model

We will use the glm function to build our logistic regression model, fitting it to our training data. 

​logistic_model <- glm(Target ~ ., data = train_data, family = binomial)

summary(logistic_model)

You might notice that some of the variables are not statistically significant, especially the dummy variables we created earlier. 

While individual dummy variables might not be significant, the overall categorical variable can still be relevant.

​Evaluating the Model

Evaluating a logistic regression model isn't just about accuracy; we're also interested in its performance across various thresholds. The ROC curve, AUC, and BIC are some good metrics to consider, along with a confusion matrix.
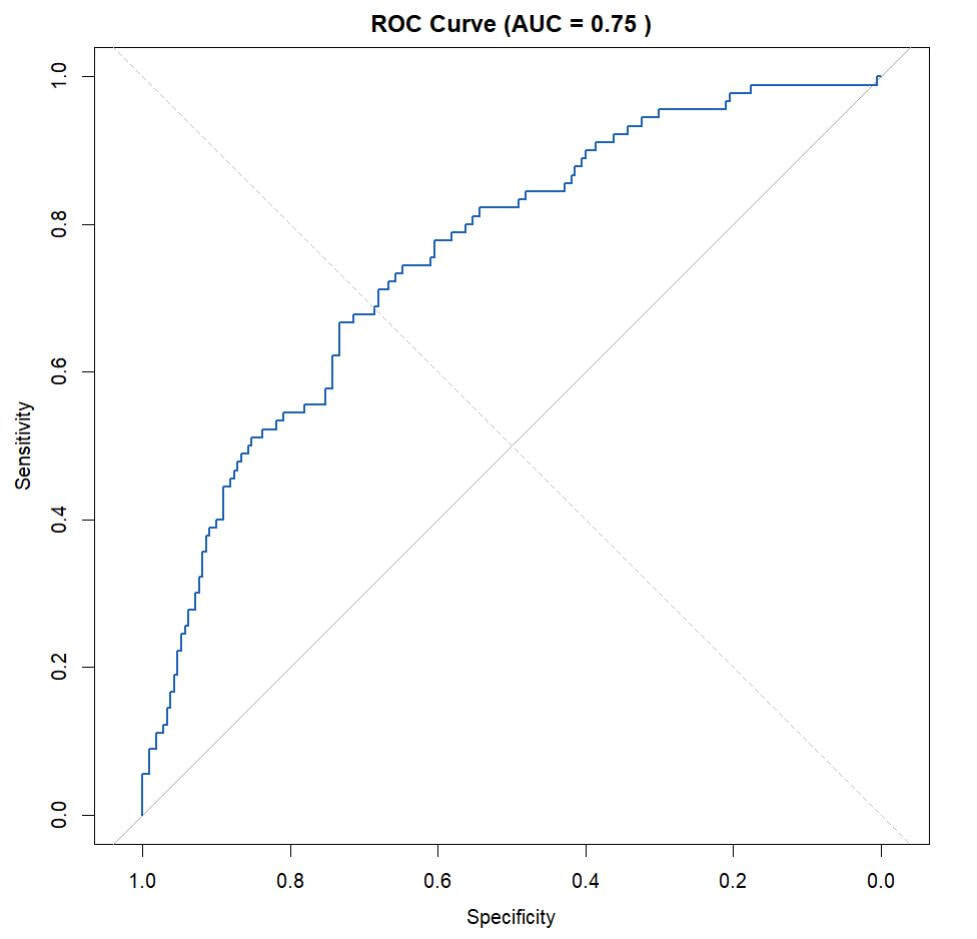
ROC CurveWe'll start by looking at the Receiver Operating Characteristic (ROC) curve, which is a graphical plot that illustrates the diagnostic ability of a binary classifier.
For this, we'll use the pROC package.

​#install.packages("pROC")
library(pROC)

predicted_probs <- predict(logistic_model, newdata=validation_data, type="response")

roc_obj <- roc(validation_data$Target, predicted_probs)
plot(roc_obj, main="ROC Curve", col="#1c61b6", lwd=2)
abline(a=0, b=1, lty=2, col="gray")  # Adding a reference line

Understanding the ROC Curve

1. Area Under the Curve (AUC): The area under the curve (AUC) is greater than 0.5, which is reassuring. An AUC of 0.5 would imply our model is no better than random guessing, like a coin flip. The higher the AUC, the better the model's performance.

2. Ideal Curve: The most ideal ROC curve would hug the top-left corner. While our curve isn't perfect, it provides a starting point for understanding our model's performance.

3. Specificity & Sensitivity:
  • When the curve is close to the bottom left (0,0) point, our model is conservative about classifying negatives. With a Specificity of 1, the model only identifies true negatives and avoids any false positives. But this also means Sensitivity is 0, and no true positives are identified.
  • On the flip side, if Sensitivity is set to 1, the model will confidently label values as Positive only when there's absolutely no risk of them being negative. The same logic applies in reverse for Specificity.

4. Interpreting AUC: The AUC represents the area between the ROC curve and a 45-degree diagonal line (known as the line of no-discrimination). This diagonal line signifies a random classifier. A larger area indicates better model performance, while a smaller area suggests our model's performance is nearing random guessing.

5. Indentation in the Curve: The indentation seen in the middle of the curve indicates areas where the model finds it challenging to distinguish between the two classes. This could mean that within this range, both the positive and negative classes have similar probability scores.
​
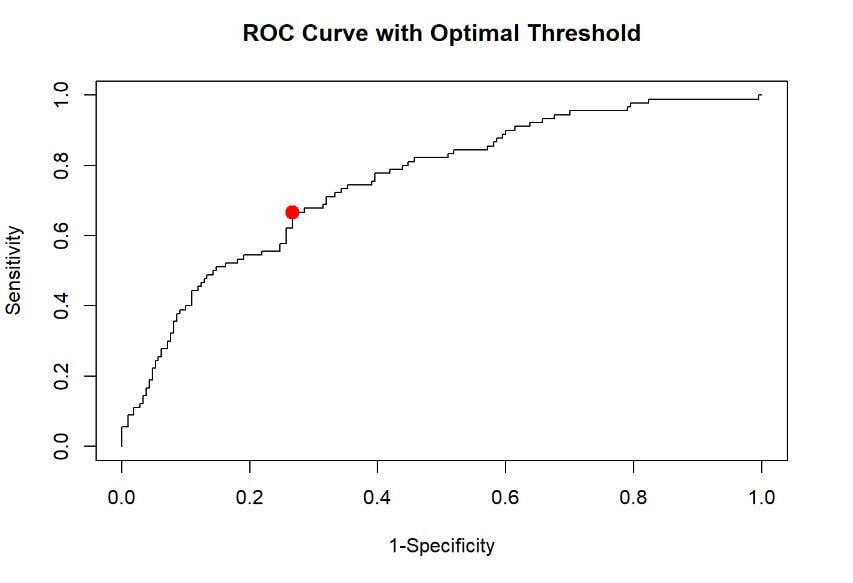
6. Finding the Optimal Threshold: The optimal threshold is found at the point on the curve closest to the top-left corner. This point represents the optimal balance between Sensitivity and Specificity for our specific needs. Once we identify this point, we can then generate a confusion matrix to further understand the model's performance.

Extracting the ROC Coordinates

Now that we've successfully plotted the ROC curve, you might wonder - how do we determine the ideal threshold for our classifier? The answer lies in Youden's Index!

Youden's Index Explained: Youden's index is a statistic which can help to choose an optimal threshold that balances sensitivity and specificity in a way that the total performance is maximized. It is computed as: sensitivity + specificity - 1. The threshold at which the Youden's index is maximized is often considered as the optimal threshold. You can read more about it here: 

https://en.wikipedia.org/wiki/Youden%27s_J_statistic

# Extracting the ROC Coordinates
full_coords <- coords(roc_obj, "all")
# You can access the roc_obj created to get the coordinates.
specificities <- full_coords$specificity
sensitivities <- full_coords$sensitivity
thresholds <- full_coords$threshold

​# Calculating Youden's Index
youden_indices <- sensitivities + specificities - 1

​# Finding and Plotting the Optimal Threshold
optimal_index <- which.max(youden_indices)

plot(1-specificities, sensitivities, type="l", xlim=c(0,1), ylim=c(0,1), 
     xlab="1-Specificity", ylab="Sensitivity", main="ROC Curve with Optimal Threshold")

points(1-specificities[optimal_index], sensitivities[optimal_index], col="red", pch=19, cex=1.5)

You should get an output like this, and it shows us the most ideal point on the ROC for the most balanced scores (Which we will get into later). 

Note: This is NOT the optimal point for a model that relies on a cost solution.

In many business scenarios, you will need to look for some sort of assigned cost to getting a false positive or a false negative. Imagine if a bank is trying to determine whether or not someone is able to get a loan - if they aren't able to pay off that loan - then the bank loses money. So how many applicants should we deny that could have potentially been able to pay off a loan just so we can save on the costs of people who may potentially not pay off a loan. 

​Classifying Predictions Using the Optimal Threshold

Having located the optimal threshold from the ROC curve, it's time to apply it! This threshold will guide our model in determining which instances should be classified as positive (1) or negative (0).

# Extracting the Optimal Threshold
optimal_threshold <- thresholds[optimal_index]

Here, we're simply taking the threshold corresponding to the point where Youden's index is maximized. This threshold will serve as our golden criterion for classification.

​# Classifying Predictions
predicted_classes <- ifelse(predicted_probs > optimal_threshold, 1, 0)

Constructing the Confusion Matrix

# Generating the Confusion Matrix
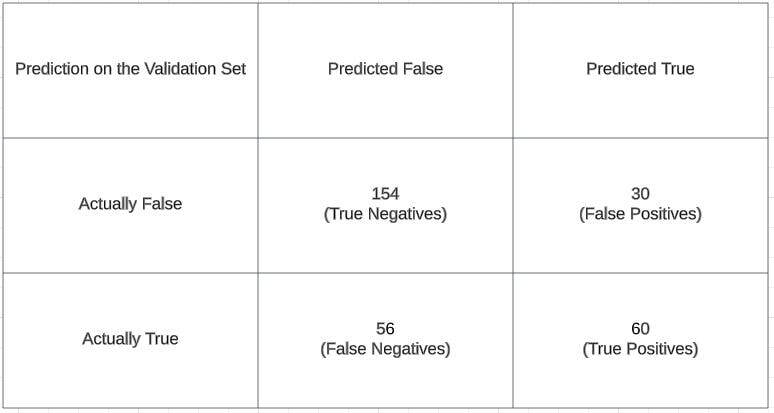
confusion_matrix <- table(predicted_classes, validation_data$Target)

# Displaying the Confusion Matrix
print(confusion_matrix)

Evaluating Classification Metrics 

After constructing our confusion matrix, it's essential to quantify our model's performance through various metrics. These metrics help us understand where the model might be excelling and where there's room for improvement.
Confusion Matrix Breakdown:
  • True Negatives (TN): The instances where the model correctly predicted the negative class.
  • False Positives (FP): The instances where the model falsely predicted the positive class.
  • False Negatives (FN): The instances where the model falsely predicted the negative class.
  • True Positives (TP): The instances where the model correctly predicted the positive class.

Note: Note how I used the validation set. When we make models, we often test things on our validation set since the model was trained on the training set. The validation set is meant to act as "unseen" data so that you can evaluate the model's performance - sometimes another split called a "test" set is used as another layer of checking model performance. 

# Given confusion matrix values
TN <- 154
FP <- 30
FN <- 56
TP <- 60

# Calculate Accuracy
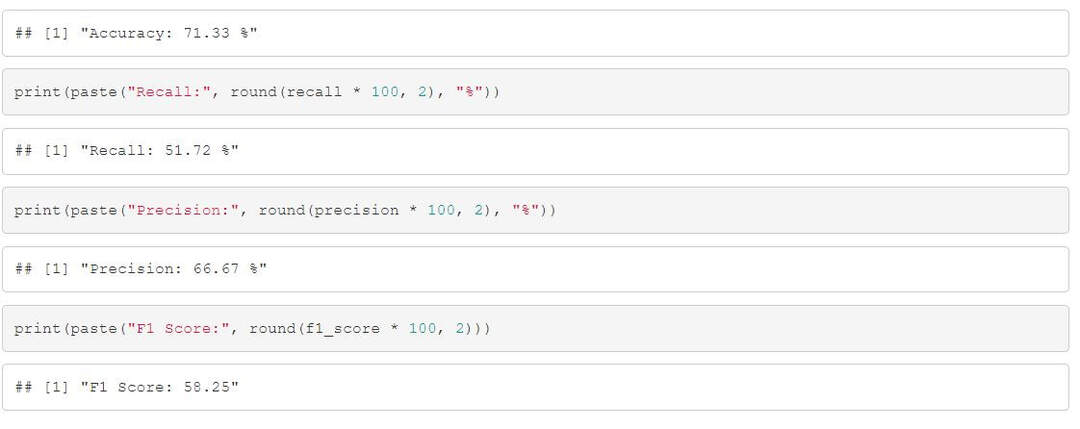
accuracy <- (TP + TN) / (TP + TN + FP + FN)
print(paste("Accuracy:", accuracy))

# Calculate Precision
precision <- TP / (TP + FP)
print(paste("Precision:", precision))

# Calculate Recall
recall <- TP / (TP + FN)
print(paste("Recall:", recall))

# Calculate F1 Score
f1_score <- 2 * (precision * recall) / (precision + recall)
print(paste("F1 Score:", f1_score))

Assuming Costs Associated

​
In many real business cases, you will situations where it costs money for the business to misclassify predictions. Take for instance these examples:

Healthcare Diagnostics:
  • Scenario: A CNN model is estimating if a tumor growth is benign or not in a patient's scans. 
  • Misclassification Costs:
    • False Positive: Diagnosing a healthy person as having a tumor growth might lead to unnecessary treatments, stress, and medical costs. This can also lead to potential legal issues.
    • False Negative: Failing to diagnose a sick person can lead to the progression of a disease, or more severe health complications
  • Business Impact: Incorrect diagnoses can lead to increased medical costs, potential lawsuits, and a damaged reputation for the healthcare provider or diagnostic tool manufacturer.

This is exactly the kind of situation where getting many false positives or negatives is a pretty bad idea. You would probably look for a model with super high accuracy, but this isn't always the case. For this example, we might want to tailor a model to lean more heavily towards reducing the false negative rate. You might need to cast a wider net and overall have more false positives - and in this case it would be good because you'd be less likely to have a sick patient who wasn't captured by the model. You would want to increase recall and tailor the model around this. Accuracy is important - but we may need to trade off the other metrics as well. 

In a case like the one below, we may consider a different approach.

E-commerce Fraud Detection:
  • Scenario: E-commerce platforms employ fraud detection algorithms to identify potentially fraudulent transactions.
  • Misclassification Costs:
    • False Positive: If a legitimate transaction is flagged as fraudulent, the platform might decline the transaction or put it on hold, leading to an unhappy customer and potential loss of sales.
    • False Negative: Failing to detect an actual fraudulent transaction can lead to financial losses, chargebacks, and increased processing fees.
  • Business Impact: Not accurately detecting fraud can erode trust in the platform, lead to financial losses, and increase operational costs due to handling disputes and chargebacks.

In this case, we might want to make a model more focused on precision - and in doing so you would gain happier customers - but this does draw the risk of getting slightly more bad actors. 
For this case, we are going to build a pipeline based on the costs of a False Positive or Negative, and create a way to see the most ideal threshold for the costs involved. 
Lets set up the costs involved. I used these strange costs because I want to show in a better way how this tradeoff works for this specific model. 
We are saying the cost of a False Positive is 1.1, and a False Negative is 1.2 

​FP_Cost = 1.1  # False Positive cost
FN_Cost = 1.2  # False Negative cost

2. Setting Up the Threshold Sequence:
The aim here is to iterate over a sequence of thresholds ranging from 0 to 1 (in increments of 0.01) and determine the classification cost for each threshold. I chose .01 as a good stepping space, anything lower might be overkill for this problem. 

threshold_seq <- seq(0, 1, 0.01)

3. Data Frame for Storing Costs:
Here I made a pre-made dataframe to store all the results.

costs_df <- data.frame(threshold = numeric(length(threshold_seq)), 
                       cost = numeric(length(threshold_seq)),
                       class_0 = numeric(length(threshold_seq)),
                       class_1 = numeric(length(threshold_seq)),
                       TP = numeric(length(threshold_seq)),
                       TN = numeric(length(threshold_seq)),
                       FP = numeric(length(threshold_seq)),
                       FN = numeric(length(threshold_seq)))

4. Iterating Over Thresholds:

We create a loop now that achieves this: 
  • Classify predictions based on the current threshold.
  • Create a confusion matrix.
  • Calculate the associated cost.
  • Store results.
We can also use debugs to make sure everything makes sense. I had to use debugs here to also remove matrices where there were 0 values which turned the matrix into a 2*1

for (i in 1:length(threshold_seq)) {
  threshold <- threshold_seq[i]
  # DEBUG CHECK
  print(paste("Processing threshold:", threshold))
  
  # Step 2: Classify predictions based on the current threshold
  predicted_classes <- ifelse(predicted_probs > threshold, 1, 0)
  print(table(predicted_classes))
  # Step 3: Create a confusion matrix
  confusion_matrix <- table(Predicted = predicted_classes, Actual = validation_data$Target)
  
  # We extract the results 
  # I needed to add this error check due to the error: 
  # "[.default`(confusion_matrix, 2, 1) : subscript out of bounds"
  # This is because in some cases everything is a 1 or a 0 where the matrix doesn't have a corner to fill.
  # This probably happens at extreme cases like 0.01 or .99
  
  if (dim(confusion_matrix)[1] == 2 & dim(confusion_matrix)[2] == 2) {
    TN <- confusion_matrix[1,1]
    FP <- confusion_matrix[1,2]
    FN <- confusion_matrix[2,1]
    TP <- confusion_matrix[2,2]
  } else {
    # DEBUG STATEMENT
    print(paste("Skipping threshold:", threshold, "due to non 2x2 confusion matrix"))
    next  # this will skip the current iteration of the loop
  }
  # We create our cost function
  
  current_cost <- FN * FN_Cost + FP * FP_Cost
  # DEBUG STATEMENT
  print(paste("Cost at threshold", threshold, "is:", current_cost))
  
  # Print the confusion matrix for each iteration: 
  
  rownames(confusion_matrix) <- c("Predicted 0", "Predicted 1")
  colnames(confusion_matrix) <- c("Actual 0", "Actual 1")
  print(confusion_matrix)
  
  # Then we store our results in the empty dataframe, for each 'i'th value we store this in the dataframe.
  
  costs_df[i, "threshold"] <- threshold_seq[i]
  costs_df[i, "cost"] <- current_cost
  costs_df[i, "class_0"] <- sum(predicted_classes == 0)
  costs_df[i, "class_1"] <- sum(predicted_classes == 1)
  costs_df[i, "TP"] <- TP
  costs_df[i, "TN"] <- TN
  costs_df[i, "FP"] <- FP
  costs_df[i, "FN"] <- FN
  
  # DEBUG STATEMENT
  print(paste("Stored cost of", current_cost, "for threshold", threshold_seq[i], "at index", i))
  }
costs_df <- costs_df[costs_df$threshold != 0.0, ]

5. Identifying the Optimal Threshold:

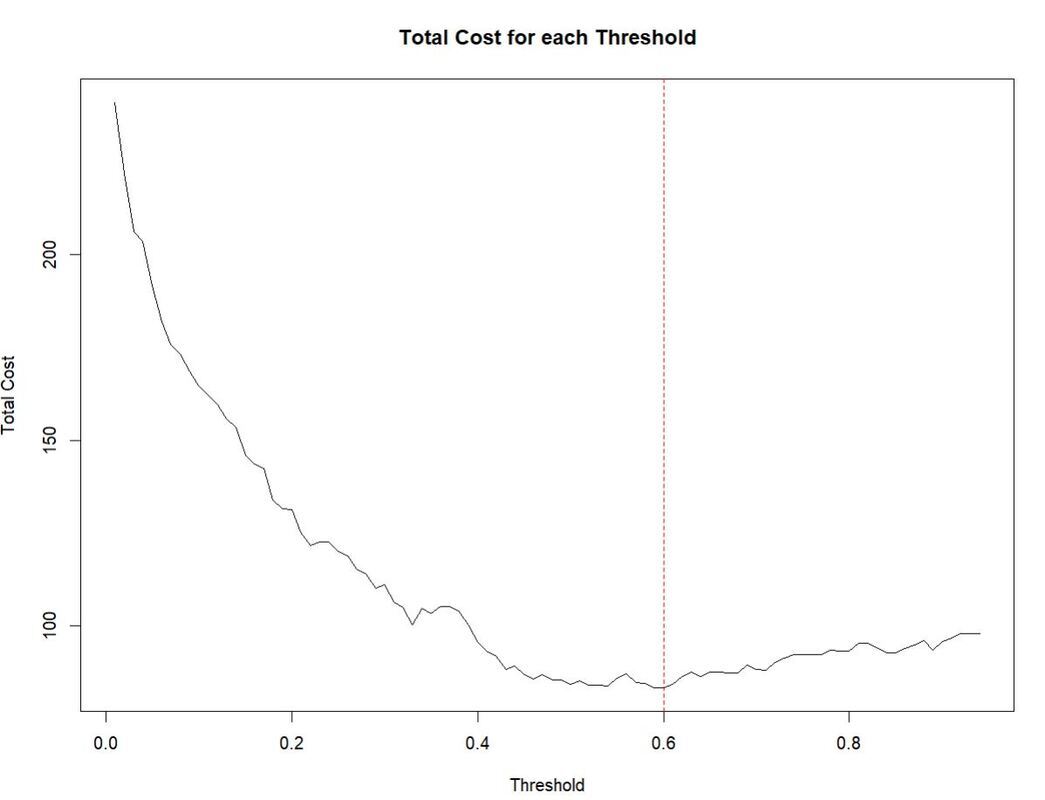
​After all thresholds are processed, we can find the one with the smallest cost.

​min_cost_row <- costs_df[costs_df$cost == min(costs_df$cost), ]
optimal_threshold_cost <- min_cost_row$threshold

6. Visualizing the Cost Trade-off

# the total costs for each threshold
plot(costs_df$threshold, costs_df$cost, type="l", xlab="Threshold", ylab="Total Cost", main="Total Cost for each Threshold")
abline(v=optimal_threshold_cost, col="red", lty=2)

Conclusion:

Thanks for reading and reviewing! We can see now that the most ideal cost solution is at the .6 threshold.